상관분석
1. 상관분석이란?
상관관계는 2개의 변수가 어떤 선형적 관계를 맺는지 분석하는 통계적 측도이며 상관 계수를 통해 두 변수 간의 선형관계 정도를 측정합니다. 상관관계는 비교를 원하는 2가지 변수만 고려하여 관계를 측정하기 때문에 그 외의 변수들은 고려하지 않는다.
- 연속 변수로 측정된 두 변수간의 선형 관계를 분석하는 기법
- 한 변수가 증가하면 다른 한 변수도 선형적으로 증가 혹은 감소하는지를 나타낸 것
→ 키와 몸무게를 통해 예를들어 보면, 위와 같은 그래프를 얻을 수 있는데 위의 그래프를 통해 키가 증가할수록 몸무게 도한 증가하는 것을 볼 수 있으며, X와 Y축에 점으로 표시한 그래프를 산점도라 일컫는다. 상관분석을 하기 위해서는 반드시 산점도를 통하여 선형성을 확인하여야 한다.
2. 상관계수 수식 및 해석
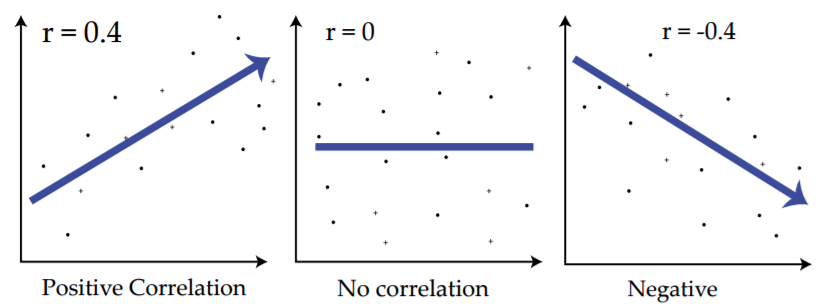
상관계수(r)는 독립변수 X와 종속변수 Y가 함께 변하는 정도를 독립변수 X와 종속변수 Y가 각각 변하는 정도로 나눈 값이다. 따라서 r값이 1이 된다면 독립변수 X와 종속변수 Y가 완전하게 같은 것이며, -1이 된다면 서로 값이 반대 부호로 완전히 같다고 보면 된다. r의 값이 0이라면 두 변수간에 선형의 상관관계가 없다라고 표현하는 것이 맞는 표현이다. 왜냐하면, 두 변수 간의 관계를 보려고 해도 두 변수의 관계가 곡선 관계라고 했을 시에는 상관분석으로는 설명이 불가하기 때문이다.
3. 상관분석 종류
- Pearson (피어슨 상관 계수
- 상관분석에서 가장 흔히 사용되는 상관계수이며, 연속형 변수와 연속형 변수 간의 선형관계를 확인할 때 사용된다. 피어슨 상관계수를 진행할때, 두 변수 모두 정규성을 따른다는 가정이 꼭 필요하다. 따라서 피어슨 상관계수는 모수적 방법이라고 지칭할 수 있다. 피어슨 상관계수 값의 범위 또한 마찬가지로,-1에서 1사이이며 해석도 위에 서술되어있듯이 똑같다.
- Spearman Rank (스피어만 순위 상관계수)
- 만약, 두 변수 모두 정규성으 만족하지 못한다면 Pearson 상관분석의 ㅣ모수 검정에 해당하는 Spearman Correlation Analysis(스퍼만 상관분석)
- Kendall Tau (켄달 Tau)
- Point-biserial (점 양분 상관계수)
- Phi (파이 계수)